Exemples de scripts en langage Python pour l’étude du modèle des gaz parfaits
Par Seraya Maouche
Dernière mise à jour : 25 mai 2025
En physique et en chimie, un gaz parfait est un modèle théorique fondamentale en thermodynamique utilisé pour décrire le comportement des gaz sous des conditions idéales. Ce modèle repose sur plusieurs hypothèses. Il permet de décrire le comportement de n’importe quel gaz à condition que l’on puisse négliger les interactions qui peuvent exister entre les particules. Comme tout modèle, celui du gaz parfait a des limites.
On rappelle l’équation d’état du modèle du gaz parfait :
Avec :
- P : Pression, exprimé en Pascal (Pa).
- V : Volume (m³)
- n : Quantité de matière exprimé en molles (mol).
- R : Constante des gaz parfaits (8,314 J · mol–1 · K–1)
- T : Température, exprimée en Kelvin (k)
Exemple 1 : Ce script permet de calculer la pression (exprimée en Pascal) à partir de l’équation du modèle du gaz parfait.
# Pression du gazn = 1 # exprimé en moles (mol)###### Formule du Gaz Parfait : p * V = n * R * TP = (n * R * T) / V
print(f"Pression du gaz : {P:.2f} Pa")Exemple 2 : Courbe P(V) lors d’une détente isotherme
Lors d’une détente isotherme, le gaz prend plus de volume (détente) pendant que la température reste constante (isotherme). Il s’agit donc d’une expansion d’un gaz à température constante. Dans ce script, nous utiliserons deux librairies Python : NumPy et Matplotlib.
- NumPy (Numerical Python) : une bibliothèque Python très populaire pour effectuer des calculs mathématiques et scientifiques en physique et en ingénierie.
- Matplotlib.pyplot : module de visualisation et de traçage de graphiques qui fait partie de la librairie Matplotlib
import numpy as np
import matplotlib.pyplot as plt
# Données physiques
n = 1 # exprimé en moles (mol)
R = 8.314 # Constante du gaz parfait
T = 300 # exprimé en Kelvin (k)V1 = 0.01 # Volume initial (en m³)
V2 = 0.05 # Volume final (en m³)
# Calcul du travail de la détente
W = n * R * T * np.log(V2 / V1)
print(f"Travail effectué lors de la détente isotherme : {W:.2f} J")
# Génération des données pour le graphique
V = np.linspace(V1, V2, 100)
P = n * R * T / V
# Affichage du graphe
plt.plot(V, P, label="P(V) = nRT / V", color="blue")
plt.title("Détente isotherme d'un gaz parfait")
plt.xlabel("Volume (m³)")
plt.ylabel("Pression (Pa)")
plt.grid(True)
plt.legend()
plt.show()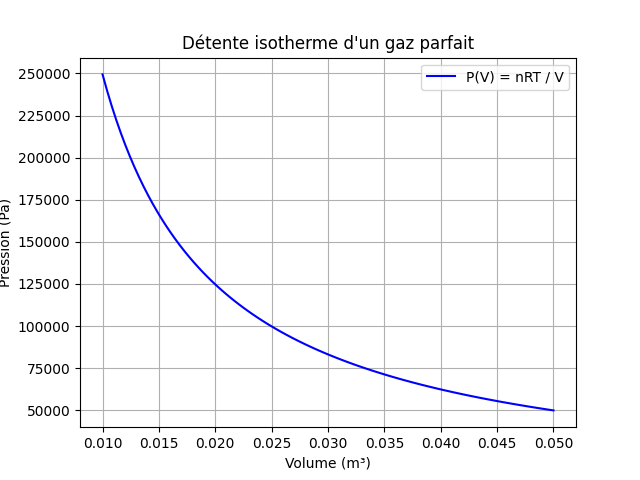
Exemple 3 : Calcul du travail d’une détente isotherme
import numpy as np
# Données
n = 1 # quantité de matière en molles
R = 8.314 # Constante des gaz parfaits
T = 300 # Température en Kelvin
Vi = 0.01 # Volume initial en m³
Vf = 0.05 # Volume final en m³
W = n * R * T * np.log(Vf / Vi)
print(f"Travail effectué lors de la détente isotherme : {W:.2f} J")Le résultat d’exécution de ce script donne : Travail effectué lors de la détente isotherme : 4014.26 J.
Exemple 4 : Évolution de la température à volume constant (isochore)
Dans cet exemple, nous utiliserons la formule suivante :
import numpy as np
import matplotlib.pyplot as plt
# Données
n = 1
R = 8.314
V = 0.03
T = np.linspace(100, 1000, 100)
P = n * R * T / V
# Affichage
plt.plot(T, P)
plt.title("Évolution de la pression en fonction de la température (isochore)")
plt.xlabel("Température (K)")
plt.ylabel("Pression (Pa)")
plt.grid(True)
plt.show()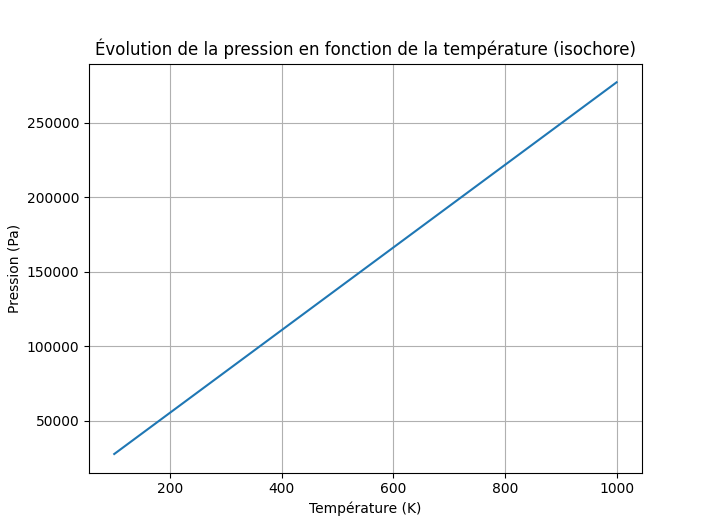
Exemple 5. Simulation du modèle du gaz parfait
import numpy as np
import matplotlib.pyplot as plt
# Constantes
R = 8.314 # Constante des gaz parfaits (J/mol·K)
n = 1 # quantité de matière en moles
T = 300 # Température en Kelvin (K)
# Variation de volume
V = np.linspace(0.1, 10, 100) # Volume de 0.1 à 10 m³
# Calcul de la pression (P = nRT/V)
P = n * R * T / V
# Visualisation
plt.figure(figsize=(8, 5))
plt.plot(V, P, 'r-', label=f'Equation du modèle des gaz parfaits (T={T} K)')
plt.xlabel('Volume (m³)')
plt.ylabel('Pression (Pa)')
plt.title('Pression en fonction du volume (Gaz parfait)')
plt.grid()
plt.legend()
plt.show()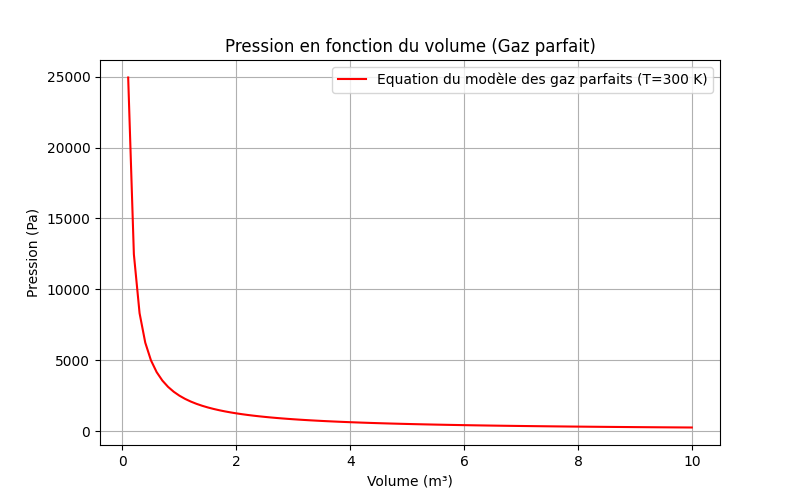
Cette figure montre la relation hyperbolique entre la pression (P) et
le volume (V) à température constante (loi de Boyle-Mariotte).